Cuando se dispone de datos de una población, y antes de abordar análisis estadísticos más complejos, un primer paso consiste en presentar esa información de forma que ésta se pueda visualizar de una manera más sistemática y resumida. Los datos que nos interesan dependen, en cada caso, del tipo de variables que estemos manejando
2.
Para variables categóricas3, como el sexo, estadio TNM, profesión, etc., se quiere conocer la frecuencia y el porcentaje del total de casos que "caen" en cada categoría. Una forma muy sencilla de representar gráficamente estos resultados es mediante diagramas de barras o diagramas de sectores. En losgráficos de sectores, también conocidos como diagramas de "tartas", se divide un círculo en tantas porciones como clases tenga la variable, de modo que a cada clase le corresponde un arco de círculo proporcional a su frecuencia absoluta o relativa. Un ejemplo se muestra en la Figura 1. Como se puede observar, la información que se debe mostrar en cada sector hace referencia al número de casos dentro de cada categoría y al porcentaje del total que estos representan. Si el número de categorías es excesivamente grande, la imagen proporcionada por el gráfico de sectores no es lo suficientemente clara y por lo tanto la situación ideal es cuando hay alrededor de tres categorías. En este caso se pueden apreciar con claridad dichos subgrupos.
Los diagramas de barras son similares a los gráficos de sectores. Se representan tantas barras como categorías tiene la variable, de modo que la altura de cada una de ellas sea proporcional a la frecuencia o porcentaje de casos en cada clase (Figura 2). Estos mismos gráficos pueden utilizarse también para describir variables numéricas discretas que toman pocos valores (número de hijos, número de recidivas, etc.).
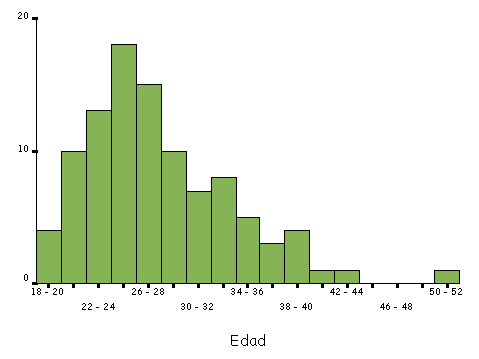
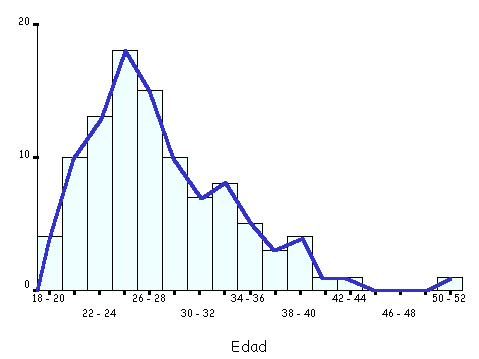
Para variables numéricas continuas, tales como la edad, la tensión arterial o el índice de masa corporal, el tipo de gráfico más utilizado es el histograma. Para construir un gráfico de este tipo, se divide el rango de valores de la variable en intervalos de igual amplitud, representando sobre cada intervalo un rectángulo que tiene a este segmento como base. El criterio para calcular la altura de cada rectángulo es el de mantener la proporcionalidad entre las frecuencias absolutas (o relativas) de los datos en cada intervalo y el área de los rectángulos. Como ejemplo, la Tabla I muestra la distribución de frecuencias de la edad de 100 pacientes, comprendida entre los 18 y 42 años. Si se divide este rango en intervalos de dos años, el primer tramo está comprendido entre los 18 y 19 años, entre los que se encuentra el 4/100=4% del total. Por lo tanto, la primera barra tendrá altura proporcional a 4. Procediendo así sucesivamente, se construye el histograma que se muestra en la Figura 3. Uniendo los puntos medios del extremo superior de las barras del histograma, se obtiene una imagen que se llama polígono de frecuencias. Dicha figura pretende mostrar, de la forma más simple, en qué rangos se encuentra la mayor parte de los datos. Un ejemplo, utilizando los datos anteriores, se presenta en la Figura 4.
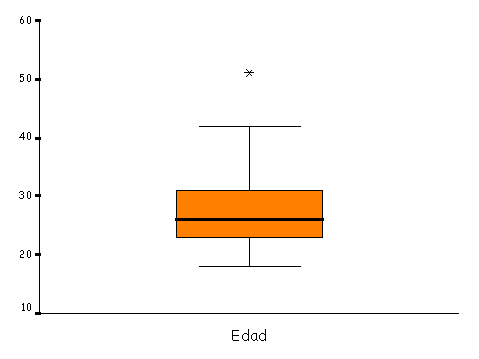
Otro modo habitual, y muy útil, de resumir una variable de tipo numérico es utilizando el concepto de percentiles, mediante diagramas de cajas4,5. LaFigura 5 muestra un gráfico de cajas correspondiente a los datos de la Tabla I. La caja central indica el rango en el que se concentra el 50% central de los datos. Sus extremos son, por lo tanto, el 1er y 3er cuartil de la distribución. La línea central en la caja es la mediana. De este modo, si la variable es simétrica, dicha línea se encontrará en el centro de la caja. Los extremos de los "bigotes" que salen de la caja son los valores que delimitan el 95% central de los datos, aunque en ocasiones coinciden con los valores extremos de la distribución. Se suelen también representar aquellas observaciones que caen fuera de este rango (outliers o valores extremos). Esto resulta especialmente útil para comprobar, gráficamente, posibles errores en nuestros datos. En general, los diagramas de cajas resultan más apropiados para representar variables que presenten una gran desviación de la distribución normal. Como se verá más adelante, resultan además de gran ayuda cuando se dispone de datos en distintos grupos de sujetos.
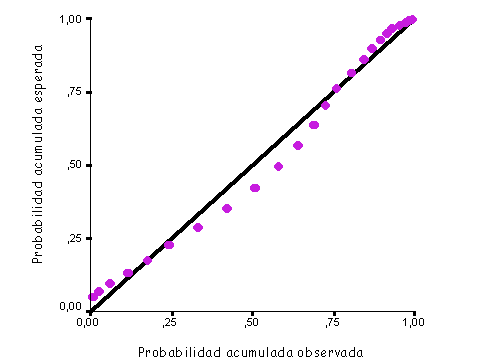
Por último, y en lo que respecta a la descripción de los datos, suele ser necesario, para posteriores análisis, comprobar la normalidad de alguna de las variables numéricas de las que se dispone. Un diagrama de cajas o un histograma son gráficos sencillos que permiten comprobar, de un modo puramente visual, la simetría y el "apuntamiento" de la distribución de una variable y, por lo tanto, valorar su desviación de la normalidad. Existen otros métodos gráficos específicos para este propósito, como son los gráficos P-P o Q-Q. En los primeros, se confrontan las proporciones acumuladas de una variable con las de una distribución normal. Si la variable seleccionada coincide con la distribución de prueba, los puntos se concentran en torno a una línea recta. Los gráficos Q-Q se obtienen de modo análogo, esta vez representando los cuantiles de distribución de la variable respecto a los cuantiles de la distribución normal. En la Figura 6se muestra el gráfico P-P correspondientes a los datos de la Tabla I que sugiere, al igual que el correspondiente histograma y el diagrama de cajas, que la distribución de la variable se aleja de la normalidad.
Figura 1. Ejemplo de gráfico de sectores. Distribución de una muestra de pacientes según el hábito de fumar. |
|
Figura 2. Ejemplo de gráfico de barras. Estadio TNM en el cáncer gástrico. |
|
Tabla I. Distribución de frecuencias
de la edad en 100 pacientes. |
Edad | Nº de pacientes |
18 | 1 |
19 | 3 |
20 | 4 |
21 | 7 |
22 | 5 |
23 | 8 |
24 | 10 |
25 | 8 |
26 | 9 |
27 | 6 |
28 | 6 |
29 | 4 |
30 | 3 |
31 | 4 |
32 | 5 |
33 | 3 |
34 | 2 |
35 | 3 |
36 | 1 |
37 | 2 |
38 | 3 |
39 | 1 |
41 | 1 |
42 | 1 |
Figura 3. Ejemplo de un histograma correspondiente a los datos de la Tabla I. |
|
Figura 4. Polígono de frecuencias para los datos de la Tabla I. |
|
Figura 5. Ejemplo de un diagrama de caja correspondiente a lo datos en la Tabla I. |
|
Figura 6. Gráfico P-P de normalidad para los datos de la Tabla I. |
|
Figura 7. Diagrama de barras agrupadas. Relación entre la presencia de alguna enfermedad coronaria y los antecedentes cardiacos familiares en una muestra. |
|
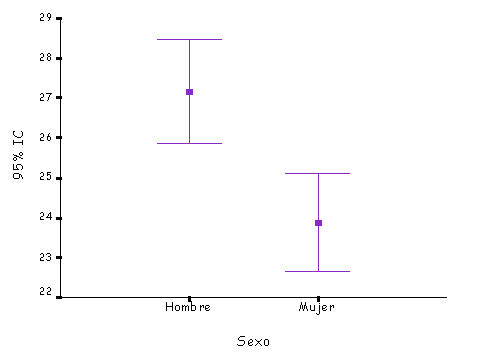
Figura 8. Barras de error. Variación en el índice de masa corporal según el sexo. |
|
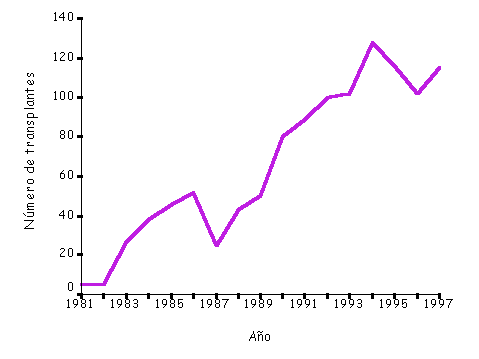
Figura 9. Gráfico de líneas. Número de pacientes trasplantados renales en el Complexo Hospitalario "Juan Canalejo" durante el periodo 1981-1997. |
|
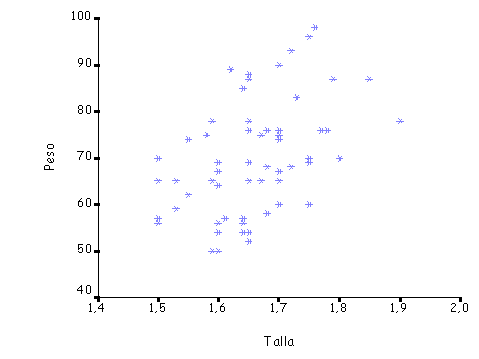
Figura 10. Diagrama de dispersión entre la talla y el peso de una muestra de individuos. |
|
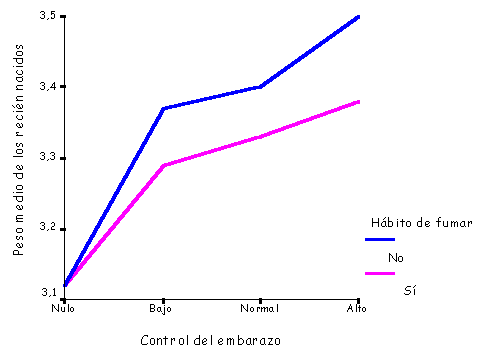
Figura 11. Dos diagramas de líneas superpuestos. Variación en el peso medio de una muestra de recién nacidos según el control ginecológico del embarazo y el hábito de fumar de la madre. |
|
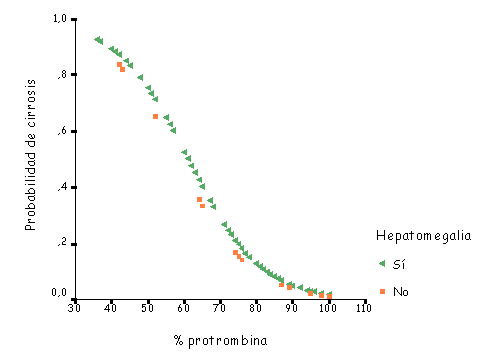
Figura 12. Diagrama de dispersión (regresión logística). Probabilidad de padecer cirrosis hepática, según un modelo de regresión logística ajustando por el % de protrombina y el presentar o no hepatomegalia. |
|
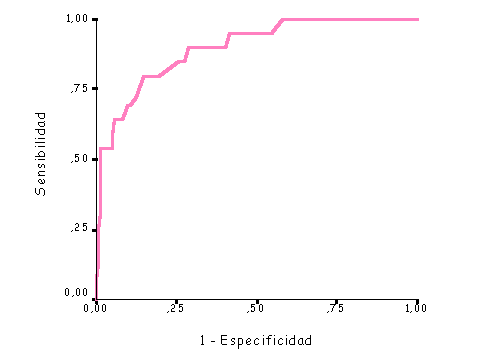
Figura 13. Curva ROC para el porcentaje de protrombina en la predicción de cirrosis. |
|
- Lang TA, Secic M. How to report statistics in medicine. Annotated Guidelines for authors, Editors, and reviewers. Philadelphia: Port City Press; 1997.
- Altman DG, Bland JM. Statistics Notes: Presentation of numerical data. BMJ 1996; 312: 572. [Medline] [Texto completo]
- Singer PA, Feinstein AR. Graphical display of categorical data. J Clin Epidemiol 1993; 46(3): 231-6. [Medline]
- Simpson RJ, Johnson TA, Amara IA. The box-plot: an exploratory analysis for biomedical publications. Am Heart J 1988; 116 (6 Part 1): 1663-5. [Medline]
- Williamson DF, Parker RA, Kendrick JS. The box plot: a simple visual method to interpret data. Ann Intern Med 1989; 110 (11): 916-21. [Medline]
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
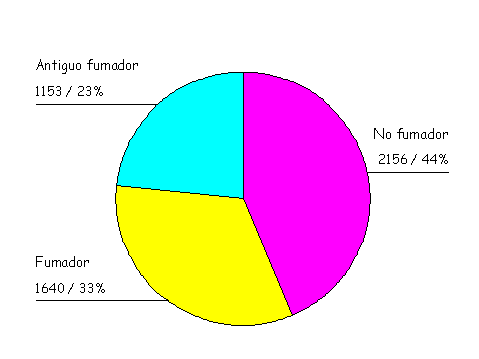
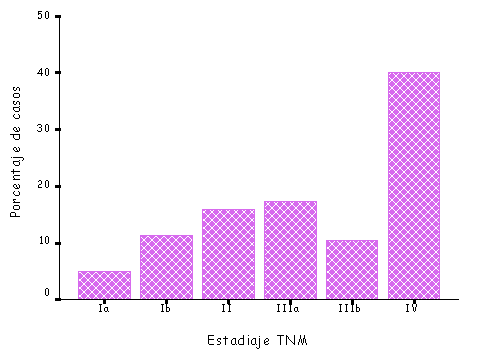
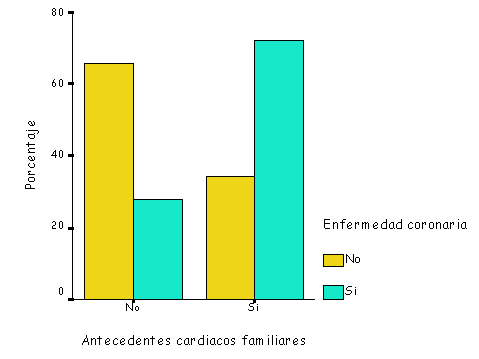
No hay comentarios:
Publicar un comentario