Probabilidad

La probabilidad mide la frecuencia con la que aparece un resultado determinado cuando se realiza un experimento.

Ejemplo: tiramos un dado al aire y queremos saber cual es la probabilidad de que salga un 2, o que salga un número par, o que salga un número menor que 4.

El experimento tiene que ser aleatorio, es decir, que pueden presentarse diversos resultados, dentro de un conjunto posible de soluciones, y esto aún realizando el experimento en las mismas condiciones. Por lo tanto, a priori no se conoce cual de los resultados se va a presentar:

Ejemplos: lanzamos una moneda al aire: el resultado puede ser cara o cruz, pero no sabemos de antemano cual de ellos va a salir.
En la Lotería de Navidad, el "Gordo" (en España se llama "Gordo" al primer premio) puede ser cualquier número entre el 1 y el 100.000, pero no sabemos a priori cual va a ser (si lo supiéramos no estaríamos aquí escribiendo esta lección).

Hay experimentos que no son aleatorios y por lo tanto no se les puede aplicar las reglas de la probabilidad.

Ejemplo: en lugar de tirar la moneda al aire, directamente selccionamos la cara. Aquí no podemos hablar de probabilidades, sino que ha sido un resultado determinado por uno mismo.

Antes de calcular las probabilidades de un experimento aleaotorio hay que definir una serie de conceptos:

Suceso elemental: hace referencia a cada una de las posibles soluciones que se pueden presentar.

Ejemplo: al lanzar una moneda al aire, los sucesos elementales son la cara y la cruz. Al lanzar un dado, los sucesos elementales son el 1, el 2, .., hasta el 6.

Suceso compuesto: es un subconjunto de sucesos elementales.

Ejemplo: lanzamos un dado y queremos que salga un número par. El suceso "numero par" es un suceso compuesto, integrado por 3 sucesos elementales: el 2, el 4 y el 6
O, por ejemplo, jugamos a la ruleta y queremos que salga "menor o igual que 18". Este es un suceso compuesto formado por 18 sucesos elementales (todos los números que van del 1 al 18).

Al conjunto de todos los posibles sucesos elementales lo denominamos espacio muestral. Cada experimento aleatorio tiene definido su espacio muestral (es decir, un conjunto con todas las soluciones posibles).

Ejemplo: si tiramos una moneda al aíre una sola vez, el espacio muestral será cara o cruz.
Si el experimento consiste en lanzar una moneda al aire dos veces, entonces el espacio muestral estaría formado por (cara-cara), (cara-cruz), (cruz-cara) y (cruz-cruz).

El concepto de probabilidad resulta familiar a cualquier profesional del ámbito sanitario, pero una definición más precisa exige considerar la naturaleza matemática de dicho concepto. La probabilidad de ocurrencia de un determinado suceso podría definirse como la proporción de veces que ocurriría dicho suceso si se repitiese un experimento o una observación en un número grande de ocasiones bajo condiciones similares. Por definición, entonces, la probabilidad se mide por un número entre cero y uno: si un suceso no ocurre nunca, su probabilidad asociada es cero, mientras que si ocurriese siempre su probabilidad sería igual a uno. Así, las probabilidades suelen venir expresadas como decimales, fracciones o porcentajes.

La definición anterior de probabilidad corresponde a la conocida como definición frecuentista. Existe otra descripción más formal desde el punto teórico que permite definir el concepto de probabilidad mediante la verificación de ciertos axiomas a partir de los que se deducen todas las demás propiedades del cálculo de probabilidades². En otros contextos, se ha defendido una interpretación más amplia del concepto de probabilidad que incluye las que podemos denominar probabilidades subjetivas o personales, mediante las cuales se expresa el grado de confianza o experiencia en una proposición. Esta definición constituye la base de los llamados métodos bayesianos, que se presentan como alternativa a la estadística tradicional centrada en el contraste de hipótesis^9-11. No obstante, y en relación con el propósito de este trabajo, bastará con considerar la definición frecuentista anterior. Así, a partir de una población con N elementos, de los cuales k presentan una característica  A, se estimará la probabilidad de la característica A como P(A) = k/N. Así, por ejemplo, en una población de 100 pacientes, 5 de los cuales son diabéticos, la probabilidad de padecer diabetes p(Diabetes) se estimará como el cocient:e 5/100= 0.5.
Es conveniente conocer algunas de las propiedades básicas del cálculo de probabilidades:

• Para un suceso A, la probabilidad de que suceda su complementario (o equivalentemente, de que no suceda A) es igual a uno menos la probabilidad de A:

donde  denota al suceso contrario o suceso complementario de A.

• Si un fenómeno determinado tiene dos posibles resultados A y B mutuamente excluyentes (es decir, que no pueden darse de forma simultánea, como ocurre en el lanzamiento de una moneda al aire), la probabilidad de que una de esas dos posibilidades ocurra se calcula como la suma de las dos probabilidades individuales:

(1)

La extensión de la ley aditiva anterior al caso de más de dos sucesos mutuamente excluyentes A, B, C... indica que:

Consideremos, como ejemplo, un servicio de urología en el que el 38,2% de los pacientes a los que se les practica una biopsia prostática presentan una hiperplasia benigna (HB), el 18,2% prostatitis (PR) y en un 43,6% el diagnóstico es de cáncer (C). La probabilidad de que en un paciente que se somete a una biopsia de próstata no se confirme el diagnóstico de cáncer prostático será igual a:

Es decir, en un 56,4% de los casos se logra descartar un diagnóstico maligno. De modo equivalente, la probabilidad anterior podría haberse calculado como la probabilidad del suceso contrario al del diagnóstico de cáncer:

Nótese la importancia del hecho de que los sucesos anteriores sean mutuamente excluyentes. Sin esta condición, la ley de adición no será válida. Por ejemplo, se sabe que en una determinada Unidad de Cuidados Intensivos (UCI) el 6,9% de los pacientes que ingresan lo hacen con una infección adquirida en el exterior, mientras que el 13,7% adquieren una infección durante su estancia en el hospital. Se conoce además que el 1,5% de los enfermos ingresados en dicha unidad presentan una infección de ambos tipos. ¿Cuál será entonces la probabilidad de que un determinado paciente presente una infección de cualquier tipo en UCI? Para realizar el cálculo, si se suman simplemente las probabilidades individuales (0,069+0,137) la probabilidad de un suceso doble (infección comunitaria y nosocomial) se estará evaluando dos veces, la primera como parte de la probabilidad de padecer una infección comunitaria y la segunda como parte de la probabilidad de adquirir una infección en la UCI. Para obtener la respuesta correcta se debe restar la probabilidad del doble suceso. Así:

• Si un fenómeno determinado tiene dos posibles resultados A y B, la probabilidad de que una de esas dos posibilidades ocurra viene dada, en general, por la expresión:

Por lo tanto, si dos o más sucesos no son mutuamente excluyentes, la probabilidad de que ocurra uno de ellos o ambos se calcula sumando las probabilidades individuales de que ocurra una de esas circunstancia, pero restando  la probabilidad de que ocurra la común.
Resulta evidente que, para el caso de procesos mutuamente excluyentes,  y se obtiene (1).
En el ejemplo anterior, la probabilidad de infección en UCI vendrá dada, por lo tanto, como:

Es decir, 19 de cada 100 enfermos registrará alguna infección (ya sea de tipo comunitario o nosocomial) durante su ingreso en la citada unidad.
A veces, la probabilidad de que un determinado suceso tenga lugar depende de que otro suceso se haya producido o no con anterioridad. Esto es, en ocasiones el hecho de que se produzca un determinado fenómeno puede hacer más o menos probable la aparición de otro. Este tipo de probabilidades se denominan probabilidades condicionadas, y se denotará por  a la probabilidad condicionada del suceso A suponiendo que el suceso B haya ocurrido ya.

• La ley multiplicativa de probabilidades indica que la probabilidad de que dos sucesos A y B ocurran simultáneamente es igual a:

(3)

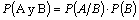
La ley multiplicativa anterior se utiliza también con el fin de determinar una probabilidad condicional  a partir de los valores de  y :

(4)

Supongamos, por ejemplo, que queremos estudiar la incidencia del hecho de ser fumador como factor de riesgo en el desarrollo de una enfermedad en una determinada población. Para ello se diseñó un estudio prospectivo y, tras seleccionar una muestra de 180 sujetos, los resultados son los que se muestran en la Tabla 1.

Tabla 1. Asociación entre el hábito tabáquico y el desarrollo de una enfermedad. Datos de un estudio de seguimiento en 180 individuos.
	Enfermos	Sanos	Total:
Fumador	60	10	70
No fumador	20	90	110
Total:	80	100	180

Considerando toda la muestra, la probabilidad de desarrollar la enfermedad (E) en la población de estudio es:

Mientras que la probabilidad de padecer la enfermedad un fumador (F) es:

Y un no fumador:

Teniendo en cuenta que:

Podría haberse aplicado la fórmula (4) para obtener cualquiera de las dos probabilidades condicionadas anteriores, resultando idénticos valores:

En el ejemplo, se constata por lo tanto que la incidencia de la enfermedad es diferente en la población fumadora que en la no fumadora (85,7% vs 18,2%). Así pues, la probabilidad de desarrollar la enfermedad depende de si se es o no fumador. En otras ocasiones, sin embargo, sucede que la ocurrencia o no de un determinado fenómeno B no influye en la ocurrencia de otro suceso A. Se dice entonces que los sucesos A y B son independientes y se verificará que:

(5)

Sustituyendo (5) en (3) se obtiene entonces que:

Es decir, en caso de independencia, la probabilidad de que ocurran dos sucesos de forma simultánea es igual al producto de las probabilidades individuales de ambos sucesos.Así, dos sucesos son independientes, si el resultado de uno no tiene efecto en el otro; o si el que ocurra el primero de ellos  no hace variar la probabilidad de que se de el segundo.
Obviamente, en la práctica, y debido a las variaciones en el muestreo, será extremadamente difícil encontrar una muestra que reproduzca de forma exacta las condiciones de independencia anteriores. El determinar si las diferencias observadas son o no compatibles con la hipótesis de independencia constituye uno de los principales problemas que aborda la estadística inferencial.

• Si se considera un fenómeno con k resultados posibles, mutuamente excluyentes, B₁, B₂,...,B_k y se conoce la probabilidad de cada uno de ellos, el llamado Teorema de las Probabilidades Totales permite calcular la probabilidad de un suceso A a partir de las probabilidades condicionadas:

Utilizando la expresión para el cálculo de la probabilidad de la intersección de dos sucesos se tiene que  y, por lo tanto:

En el ejemplo anterior, podría aplicarse este resultado para el cálculo de la incidencia de la enfermedad en la población de estudio:

Las leyes aditiva y multiplicativa, junto con la noción de probabilidades condicionadas y el teorema de las probabilidades totales se han empleado para desarrollar el llamado Teorema de Bayes, de indudable interés en la aplicación de la estadística al campo de la medicina. Si se parte de la definición de probabilidad condicionada (4):

ó

siempre que  y . Aplicando además el teorema de las probabilidades totales se llega a que:

El diagnóstico médico constituye un problema típico de aplicación del Teorema de Bayes en el campo médico, puesto que permite el cálculo de la probabilidad de que un paciente padezca una determinada enfermedad una vez dados unos síntomas concretos. La capacidad predictiva de un test o de una prueba diagnóstica suele venir dada en términos de su sensibilidad y especificidad¹². Tanto la sensibilidad como la especificidad son propiedades intrínsecas a la prueba diagnóstica, y definen su validez independientemente de cuál sea la prevalencia de la enfermedad en la población a la cual se aplica. Sin embargo, carecen de utilidad en la práctica clínica, ya que sólo proporcionan información acerca de la probabilidad de obtener un resultado concreto (positivo o negativo) en función de si un paciente está realmente enfermo o no. Por el contrario, el concepto de valores predictivos, a pesar de ser de enorme utilidad a la hora de tomar decisiones clínicas y transmitir información sobre el diagnóstico, presenta la limitación de que dependen en gran medida de lo frecuente que sea la enfermedad a diagnosticar en la población objeto de estudio. El Teorema de Bayes permite obtener el valor predictivo asociado a un test al aplicarlo en poblaciones con índices de prevalencia muy diferentes.
Consideremos como ejemplo un caso clínico en el que una gestante se somete a la prueba de sobrecarga oral con 50 gramos de glucosa para explorar la presencia de diabetes gestacional, obteniéndose un resultado positivo. Es sabido que dicho test presenta unos valores aproximados de sensibilidad y especificidad en torno al 80% y al 87%, respectivamente. Si se conoce además que la prevalencia de diabetes gestacional en la población de procedencia es aproximadamente de un 3%, por medio del teorema de Bayes podemos conocer la probabilidad de que el diagnóstico sea correcto o, equivalentemente, el valor predictivo positivo:

Se puede concluir por lo tanto que, a pesar de obtener un resultado positivo en la prueba, existe sólo una probabilidad de un 15,9% de que la paciente padezca diabetes gestacional.
Supongamos que además dicha paciente tiene más de 40 años de edad. Se sabe que en grupos de edad más avanzada la prevalencia de diabetes gestacional entre las gestantes llega a aumentar hasta aproximadamente un 8%. En este caso, el valor predicativo positivo asociado vendrá dado por:

En este caso las posibilidades de un diagnóstico de diabetes gestacional aumentan hasta un 34,86%.
En un caso como este, en que se realiza una prueba para obtener información sobre un diagnóstico, suele hablarse de probabilidad a priori, que es la disponible antes de realizar la prueba (la prevalencia, en este caso) y probabilidad a posteriori, que es la obtenida después de realizarla (los valores predictivos). A su vez, se suele denominar verosimilitudes a las probabilidades de un suceso bajo distintas hipótesis. El teorema de Bayes permite así obtener los valores de las probabilidades a posteriori a partir de las probabilidades a priori mediante una multiplicación proporcional a las verosimilitudes.
Tal y como se indicó al inicio del presente artículo, la teoría de la probabilidad constituye la base matemática para la aplicación de la estadística inferencial en medicina. El cálculo de probabilidades constituye una herramienta que permitirá hacer inferencia sobre distintos parámetros poblacionales a partir de los resultados obtenidos en una muestra, y después tomar decisiones con el mínimo riesgo de equivocación en situaciones de incertidumbre.

Bibliografía

1. Argimón Pallás JM, Jiménez Villa J. Métodos de investigación clínica y epidemiológica. 2ª ed. Madrid: Harcourt; 2000.
2. Sentís J, Pardell H, Cobo E, Canela J. Bioestadística. 3ª ed. Barcelona: Masson; 2003.
3. Colton T. Estadística en medicina. Barcelona: Salvat; 1979.
4. Armitage P, Berry G. Estadística para la investigación biomédica. Barcelona: Doyma; 1992.
5. Departamento de Medicina y Psiquiatría. Universidad de Alicante. Tratado de Epidemiología Clínica. Madrid: DuPont Pharma; 1995.
6. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall; 2004.
7. Vélez R, Hernández V. Cálculo de Probabilidades I. Madrid: UNED; 1995.
8. Quesada V, García A. Lecciones de Cálculo de Probabilidades. Madrid: Díaz de Santos; 1988.
9. Silva LC, Benavides A. El enfoque bayesiano: otra manera de inferir. Gac Sanit 2001; 15(4): 341-346.
10. Silva LC, Suárez P. ¿Qué es la inferencia bayesiana? JANO 2000; 58: 65-66.
11. Silva LC, Muñoz A. Debate sobre métodos frecuentistas vs bayesianos. Gac Sanit 2000; 14: 482-494.
12. Pértega Díaz S, Pita Fernández S. Pruebas diagnósticas. Cad Aten Primaria 2003; 10: 120-124.